Computers have helped mathematical research accelerate in multiple directions and increased the presence of mathematics in everyday life.
The role of technology in teaching and learning mathematics is increasingly on my mind as a math instructor who sees new students arrive at Simon Fraser University (SFU) every year. Both at SFU, and when I visit Canadian math classrooms as a guest speaker, I look out into rooms filled with vibrant young people surrounded by calculators, computers and smart phones.
And that’s OK. Like many mathematicians, I have not pushed back against the new technological winds ushered forward by modern times. But such technology should enhance and extend, rather than replace, the ability to think mathematically.
Adieu geometry?
Recently, I met with a young person who was interested in math and computing, but not certain which direction he would like to go in. I offered the following problem used by the University of Oxford to interview undergraduate mathematics candidates:
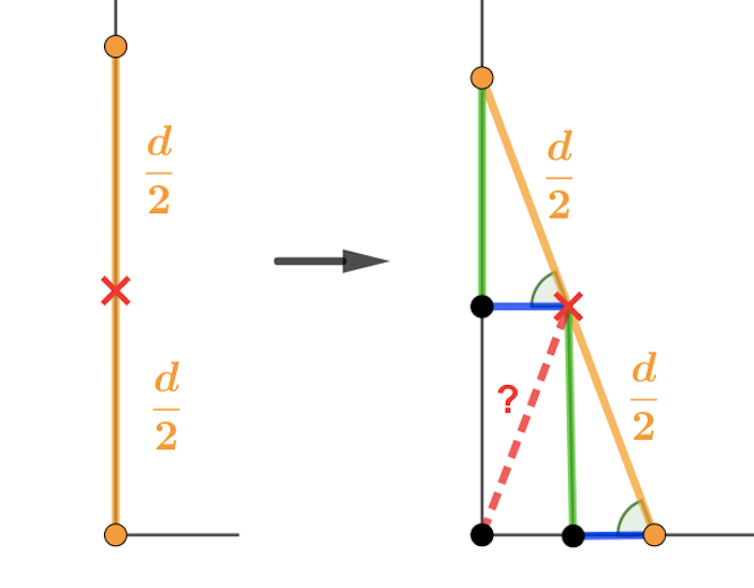
“Imagine a ladder leaning against a vertical wall with its feet on the ground. The middle rung of the ladder has been painted a different colour on the side, so that we can see it when we look at the ladder from the side on. What shape does that middle rung trace out as the ladder falls to the floor?”
One way to approach the ladder puzzle is to use, in a relatively simple way, Euclidean geometry, to show that the answer is a quarter of a circle. See below:
Rather than draw on geometrical properties, the young man used the Python programming language to animate the problem and find the required shape. He had learned Python on his own earlier that summer. When I asked him about congruent triangles, the young man looked perplexed.
Situations like this make me fear that if not used with due care in classrooms, technology may deprive students of fully developing their numeracy and spatial skills.
Unreachable problems
What mathematicians call “the computationally assisted approach” has enabled researchers to explore and solve mathematical problems that would otherwise be unreachable. The computer-assisted proof of the celebrated Four Colour Theorem comes to mind.
But some mathematical questions have demonstrated limitations of existing technology — and the fact that some solutions are dependent largely on human intuition, inspiration and intelligence. One such problem, known as the party problem (yes, as in a dinner party), is finding the number of guests that would guarantee that one always can find six people who are mutual friends or six people who are mutual strangers.
In mathematical terms, this problem is about finding what’s called “the Ramsey number R(6,6),” related to a branch of mathematics that studies what conditions must exist for a given pattern to appear.
Believe it or not, since 1930 mathematicians have know that R(6,6) exists; since 1994 we have known this number is between 102 and 165.
No progress since!
Experimental mathematics
Celebrated Canadian mathematicians and brothers Peter Borwein and Jonathan Borwein — who established the Centre for Experimental and Constructive Mathematics in 1993 at SFU — were among research pioneers who contributed to the process of aligning mathematics and new technologies.
As suggested by Jonathan Borwein and mathematician David H. Bailey, experimental mathematics uses “a computationally assisted approach to mathematical research.” They meant experimental math is about using computers to boost processes that have been the basic elements of mathematical research for centuries:
- Gaining insight and intuition;
- Visualizing mathematical principles;
- Discovering new relationships;
- Testing and especially falsifying conjectures;
- Exploring a possible result to make an evidence-based decision if the possible result merits formal proof;
- Suggesting approaches for formal proof.
They also argued computers could help with performing lengthy mathematical derivations and confirming analytically derived results.
Their point was that computers enable researchers to push their explorations into new or different dimensions.
New exploration
Bailey and Borwein’s ideas may be used to help describe contemporary and future ways of teaching mathematics to help students look at problems in new ways.

In my geometry-Python anecdote, I might have challenged the student by observing that the shape obtained by the Python-generated animation only looks like a quarter circle (this may refer to points 1-3 and 5 in the Bailey-Borwein definition) and that a complete answer would require an analytically derived result (point 6).
To justify the challenge, I might also choose to show the student a seemingly mind-bending visual proof, such as the animation that “shows” 64 = 65.
I might conclude by quoting 17th-century mathematician and philosopher René Descartes, who resolved:
“… never to accept anything for true which I did not clearly know to be such; that is to say, carefully … avoid … prejudice, and to comprise nothing more in my judgment than what was presented to my mind so clearly and distinctly as to exclude all ground of doubt.”
Experimental mathematics curricula
Researchers and educators have developed curricula specializing in teaching children and youth how to use computers to enhance and extend their own mathematical learning and thinking in Canadian high schools. For example, The RabbitMath Curriculum Project, led by mathematician Peter Taylor of Queen’s University and Chris Suurtamm of the University of Ottawa, or the Callysto Project, championed by the Pacific Institute for Mathematical Sciences (PIMS) and the Alberta-based not-for-profit organization Cybera.
The challenge for the mathematics teaching community will be about increasingly creating and sustaining a healthy balance in our classrooms between the power of rigorous, formal mathematics and the power of computing.
When I think of the future, I am concerned that the rigorous and formal parts of mathematics could fade away and be left outside students’ scope.
For a student in the not-too-distant future, would, for example, the number pi become a rational number — meaning, would it be equal to its approximation generated by the most powerful computer at the moment?
Most importantly, what will all this mean to students and their learning of mathematics as an instrument to better navigate the world around them?![]()







